Operations on Sets

1. Union

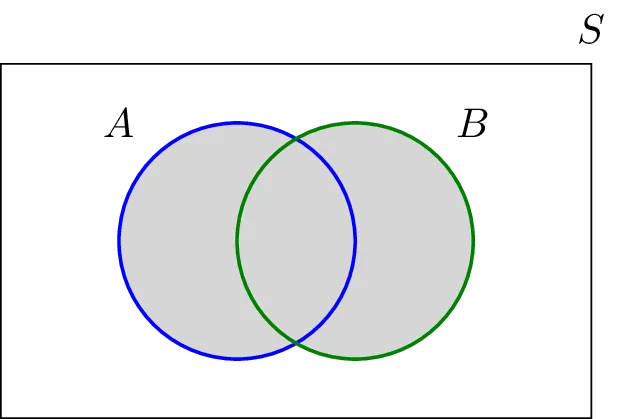
The union of two sets is a set containing all elements that are in A or in B (possibly both). For example,

{1,2} ∪ {2,3} = {1,2,3}

2. Intersection

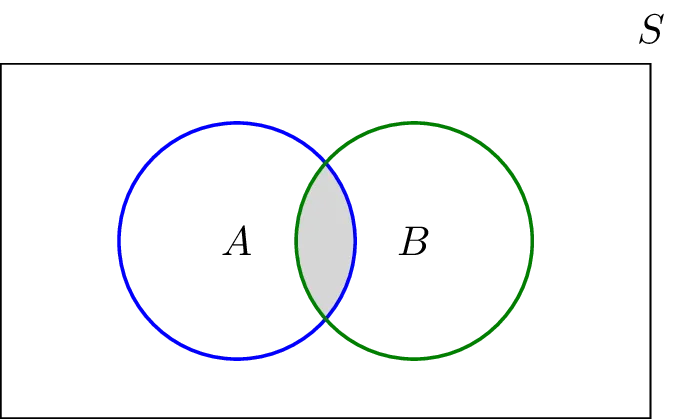
The intersection of two sets A and B, denoted by A∩B, consists of all elements that are both in A and B. For example,

{1,2} ∩ {2,3} = {2}

The intersection of A and B is the middle part

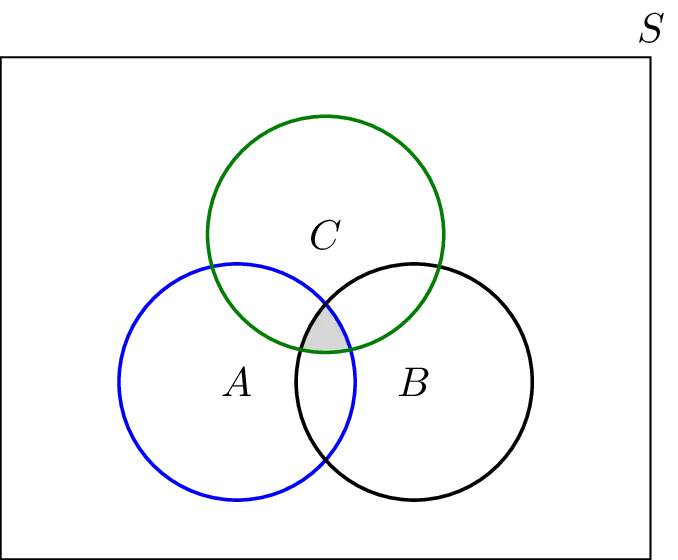
3. Disjoint

Set A and set B are called disjoint sets if no element is common to A and B. i.e. A and B are disjoint sets then

(A ∩ B = ∅)

For example, A = {1,3,5}, B = {2,4,6} and C = {a,b,c}
A ∩ B ∩ C = ∅

4. Complement

The complement of a set A, denoted by A^c is elements in Universal Set which are not in A

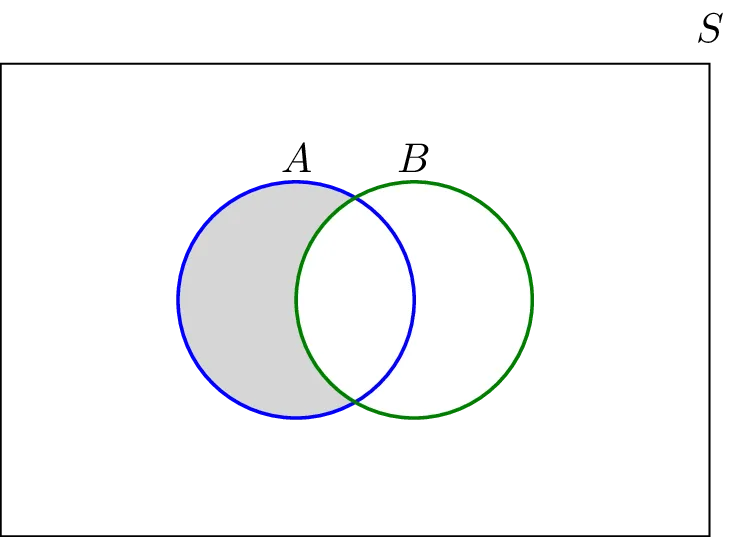
5. Difference

The set A − B consists of elements that are in A but not in B. For example if

A = {1,2,3} and B = {3,5} then,
A - B = {1,2}

Some conclusions from set operations

Let S be the universal set, and A,B,C,D are subsets of S. Then,

1. A ∪ ∅ = A

   Hence ∅ i.e. empty set is identity set for 'union operation'.



2. A ∩ S = A

   S i.e. universal set is identity set for 'intersection operation'.



3. A ∪ S = S

   A ⊂ S and A ∪ S = S

   ⇒ if B ⊂ A then A ∪ B = A i.e. union of super set and subset is super set.



4. A ∩ ∅ = ∅

   ∅ ⊂ A and A ∩ ∅ = ∅

   ⇒ if B ⊂ A then A ∩ B = B i.e. intersection of super set and subset is subset.



5. If B ⊂ A, then A ∩ B = B and A ∪ B = A


6. A ⊂ A ∪ B also B ⊂ A ∪ B


7. A ∩ B ⊂ A also A ∩ B ⊂ B


8. A ∩ B ⊂ A ⊂ A ∪ B and A ∩ B ⊂ B ⊂ A ∪ B i.e, A and B sets. A ∩ B is the smallest set and A ∪ B is largest set.

   A contains A ∩ B and A is contained in A ∪ B.

   Similarly B contains A ∩ B and B is contained in A ∪ B.



9. As A ∩ B ⊂ A

   ⇒ (A ∩ B) ∪ A = A [super set]

   and (A ∩ B) ∩ A = (A ∩ B) [subset]



10. As A ⊂ A ∪ B

    ⇒ A ∩ (A ∪ B) = A [subset]

    and A ∪ (A ∪ B) = (A ∪ B) [super set]



11. (A - B) ∪ (A ∩ B) ∪ (B - A) = A ∪ B and (A - B), (A ∩ B), (B - A) are pairwise disjoint. i.e.

    (A - B) ∩ (A ∩ B) = ∅

    (A - B) ∩ (B - A) = ∅

    (A ∩ B) ∩ (B - A) = ∅

    Hence (A - B), (A ∩ B) and (B - A) are partitions of A ∪ B.



12. A ∪ A' = S

    i.e. Union of A and its complement gives identity set for intersection operation.



13. A ∩ A' = ∅

    i.e. Intersection of A and its complement gives identity set for union operation.

Remark:

• Property 11 and 12 are very useful for Boolean algebra as in Boolean algebra these properties are formed in a way: a + a' = 1 i.e. sum of element and its complement gives multiplicative identity element and a. a' = 0


• Multiplication of element and its complement gives additive identity element.